Quy tắc hình bình hành là một trong những khái niệm quan trọng trong vật lý, đặc biệt trong lĩnh vực cơ học. Quy tắc này giúp chúng ta xác định hợp lực khi hai lực tác dụng lên một vật thể ở cùng một điểm, tạo thành một hình bình hành. Việc sử dụng quy tắc hình bình hành, người học không chỉ có thể hiểu rõ hơn về mối quan hệ giữa các lực mà còn ứng dụng nó vào thực tế.
Tổng quan về hình bình hành
Hình bình hành là một loại đa giác có bốn cạnh, trong đó hai cặp cạnh đối diện song song với nhau. Đây là một hình dạng quen thuộc và có nhiều ứng dụng trong thực tế, xuất hiện trong các lĩnh vực như kiến trúc, nghệ thuật, thiết kế và toán học.
Để nhận diện một hình bình hành, ta có thể dựa vào một số đặc điểm sau:
Một tứ giác được xem là hình bình hành nếu có hai cặp cạnh song song.
Nếu một tứ giác có hai cặp góc đối diện bằng nhau, thì hình đó là hình bình hành.
Hình bình hành cũng được xác định bởi việc hai đường chéo của nó chia nhau thành hai nửa bằng nhau.
Ngoài ra, nếu tứ giác có một cặp góc kề bù, thì đó cũng là hình bình hành.
Một số ví dụ điển hình của hình bình hành bao gồm hình vuông, hình chữ nhật và hình thoi. Tuy nhiên, không phải mọi hình bình hành đều có những tính chất đặc trưng của các hình dạng đặc biệt này.
Các tính chất của hình bình hành:
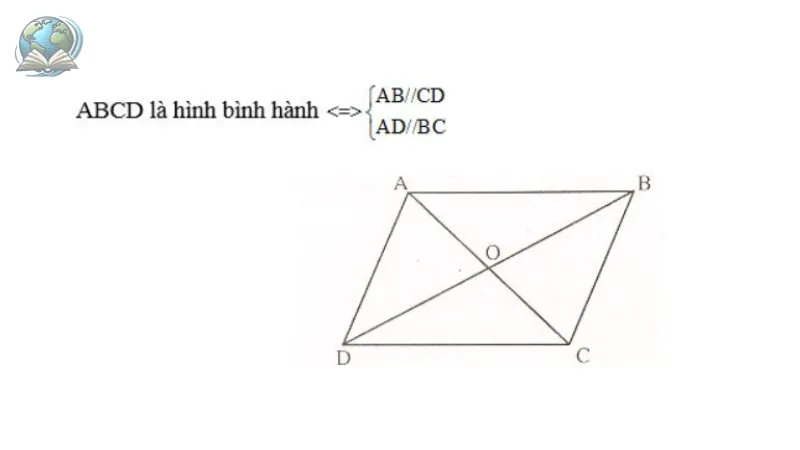
Nếu tứ giác ABCD là hình bình hành thì:
- Các cạnh đối song song và bằng nhau; AB = CD, AD = BC
- Các góc đối bằng nhau: A = C, B = D
- Hai đường chéo cắt nhau tại trung điểm của mỗi đường: OA = OC, OB = OD.
Quy tắc hình bình hành
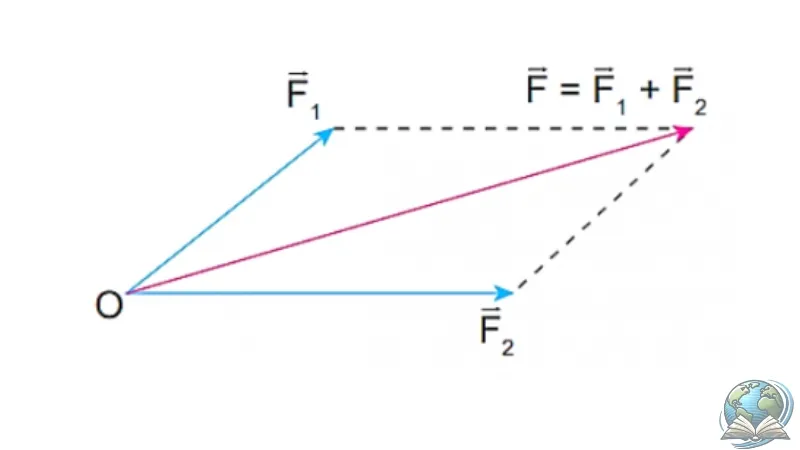
Quy tắc hình bình hành trong vật lý là một phương pháp đơn giản để xác định kết quả của hai lực tác động lên một vật. Quy tắc này nêu rõ rằng, nếu hai lực có cùng điểm tác dụng và không nằm cùng một hướng, ta có thể vẽ hai vectơ tương ứng với hai lực đó, sao cho chúng tạo thành hai cạnh kề nhau của một hình bình hành.
Kết quả của hai lực sẽ được biểu diễn bằng vector đường chéo của hình bình hành, có cùng điểm xuất phát với hai vector ban đầu. Quy tắc hình bình hành có thể áp dụng cho bất kỳ số lượng lực nào, miễn là tất cả các lực này đều có cùng một điểm tác dụng.
Phương pháp này giúp phân tích và tính toán các lực trong các tình huống phức tạp một cách dễ dàng và trực quan.
Quy tắc hình bình hành cũng được sử dụng trong toán học và vật lý để biểu diễn tổng của hai vectơ hoặc tổng hợp lực của hai lực quy đồng. Quy tắc này có thể được diễn đạt như sau:
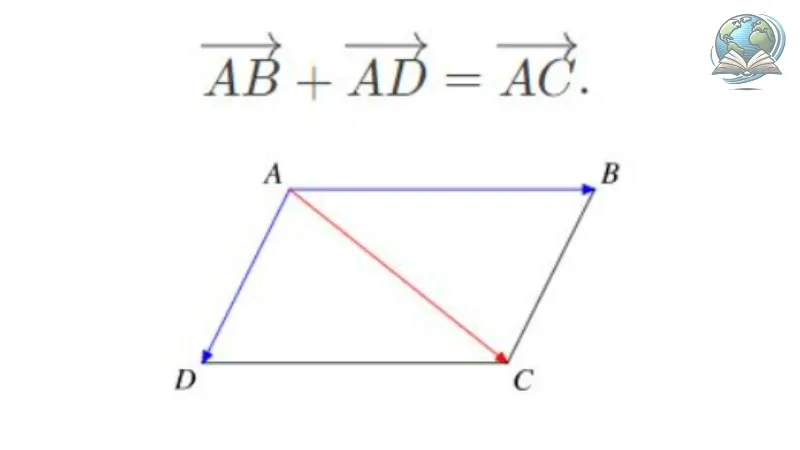
Cho hình bình hành ABCD, ta có: AB + AD = AC hoặc BC + BD = AC.
Có nghĩa là: Tổng hai vectơ có chung điểm đầu của một hình bình hành bằng với vectơ đường chéo xuất phát từ cùng một điểm.
Chứng minh: Việc chứng minh được thực hiện dựa vào hai vectơ bằng nhau cùng với quy tắc ba điểm và quy tắc trừ.
Trong vật lý, quy tắc này được áp dụng để mô tả hợp lực của hai lực quy đồng, được biểu diễn bằng đường chéo của hình bình hành mà hai cạnh là các vectơ thể hiện hai lực thành phần. Phương pháp này giúp xác định độ lớn và hướng của hợp lực một cách trực quan và đơn giản.
Ngược lại, trong một tứ giác ABCD, nếu AB + AD = AC, thì tứ giác này sẽ là hình bình hành. Từ đây, ta có thể suy ra rằng hai vectơ AB và DC có cùng hướng và độ dài bằng nhau. Như vậy, tứ giác ABCD có một cặp cạnh đối song song và bằng nhau, do đó tứ giác ABCD được xác định là hình bình hành.
Các công thức tính trong quy tắc hình bình hành
Công thức tính chu vi hình bình hành
Công thức 1:
Chu vi = 2 (a + b)
Trong đó, a và b là độ dài hai cạnh kề nhau của hình bình hành. Để tính được chu vi, ta cần biết độ dài hai cạnh kề nhau hoặc độ dài một cạnh và góc giữa hai cạnh kề nhau. Công thức này có thể được suy ra từ công thức tính chu vi hình chữ nhật, vì hình bình hành có thể được chuyển thành hình chữ nhật bằng cách cắt và dán một tam giác vuông.
Công thức 2:
Nếu biết góc giữa hai cạnh kề nhau, ta có thể sử dụng công thức:
a = c cos α
b = c sin α
Trong đó, c là độ dài đường chéo của hình bình hành, α là góc giữa đường chéo và một cạnh kề. Sau khi tính được a và b, ta thay vào công thức chu vi để tìm kết quả.
Công thức tính diện tích hình bình hành
Công thức 1:
Công thức tính diện tích hình bình hành là:
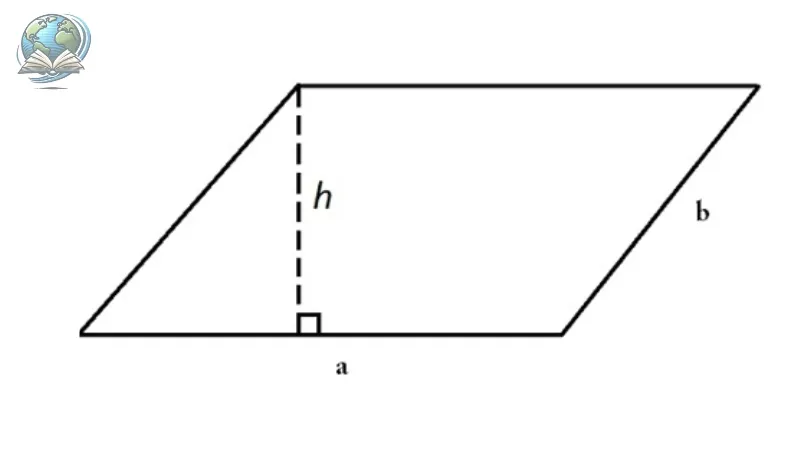
Diện tích = Chiều cao x Chiều dài cạnh đáy
Trong đó, chiều cao là khoảng cách từ một đỉnh của hình bình hành đến đường thẳng chứa cạnh đối của nó. Chiều dài cạnh đáy là độ dài của một cạnh bất kỳ của hình bình hành.
SABCD = a.h
Trong đó
S là diện tích hình bình hành
a là cạnh đáy của hình bình hành
h là chiều cao, nối từ đỉnh tới đáy của một hình bình hành
Công thức 2: Diện tích hình bình hành bằng tích của độ dài đường chéo và sin của góc giữa hai đường chéo. Công thức này có thể viết dưới dạng toán học như sau: S = d1.d2.sinα, trong đó S là diện tích, d1 và d2 là độ dài hai đường chéo, và α là góc giữa hai đường chéo.
Công thức 3: Diện tích hình bình hành bằng nửa tích của độ dài hai cạnh kề nhau và sin của góc giữa hai cạnh đó. Công thức này có thể viết dưới dạng toán học như sau: S = (1/2).a.b.sinγ, trong đó S là diện tích, a và b là độ dài hai cạnh kề nhau, và γ là góc giữa hai cạnh đó.
Tóm lại, quy tắc hình bình hành không chỉ đơn thuần là một lý thuyết trong vật lý mà còn là một công cụ hữu ích trong việc phân tích các tình huống thực tế liên quan đến lực và chuyển động. Bằng cách áp dụng quy tắc này, chúng ta có thể xác định chính xác hợp lực của nhiều lực tác dụng lên một vật thể, từ đó đưa ra những giải pháp hiệu quả trong thiết kế và thi công.
